Views on Correlation Structure — view_on

Helper to construct views on the correlation matrix.

Usage

view_on_correlation(x, cor)

# S3 method for default
view_on_correlation(x, cor)

# S3 method for matrix
view_on_correlation(x, cor)

# S3 method for xts
view_on_correlation(x, cor)

# S3 method for tbl_df
view_on_correlation(x, cor)

Arguments

x: An univariate or a multivariate distribution.
cor: A matrix for the target correlation structure of the series in x.

Value

A list of the view class.

Examples

library(ggplot2)

# Invariant
ret <- diff(log(EuStockMarkets))

# Assume that a panic event throws all correlations to the roof!
co <- matrix(0.95, 4, 4)
diag(co) <- 1
co
#>      [,1] [,2] [,3] [,4]
#> [1,] 1.00 0.95 0.95 0.95
#> [2,] 0.95 1.00 0.95 0.95
#> [3,] 0.95 0.95 1.00 0.95
#> [4,] 0.95 0.95 0.95 1.00

# Prior probability (usually the equal-weight setting)
prior <- rep(1 / nrow(ret), nrow(ret))

# View
views <- view_on_correlation(x = ret, cor = co)
views
#> # ffp view
#> Type:  View On Correlation
#> Aeq :  Dim 10 x 1859 
#> beq :  Dim 10 x 1 

# Optimization
ep <- entropy_pooling(p = prior, Aeq = views$Aeq, beq = views$beq, solver = "nlminb")
autoplot(ep)


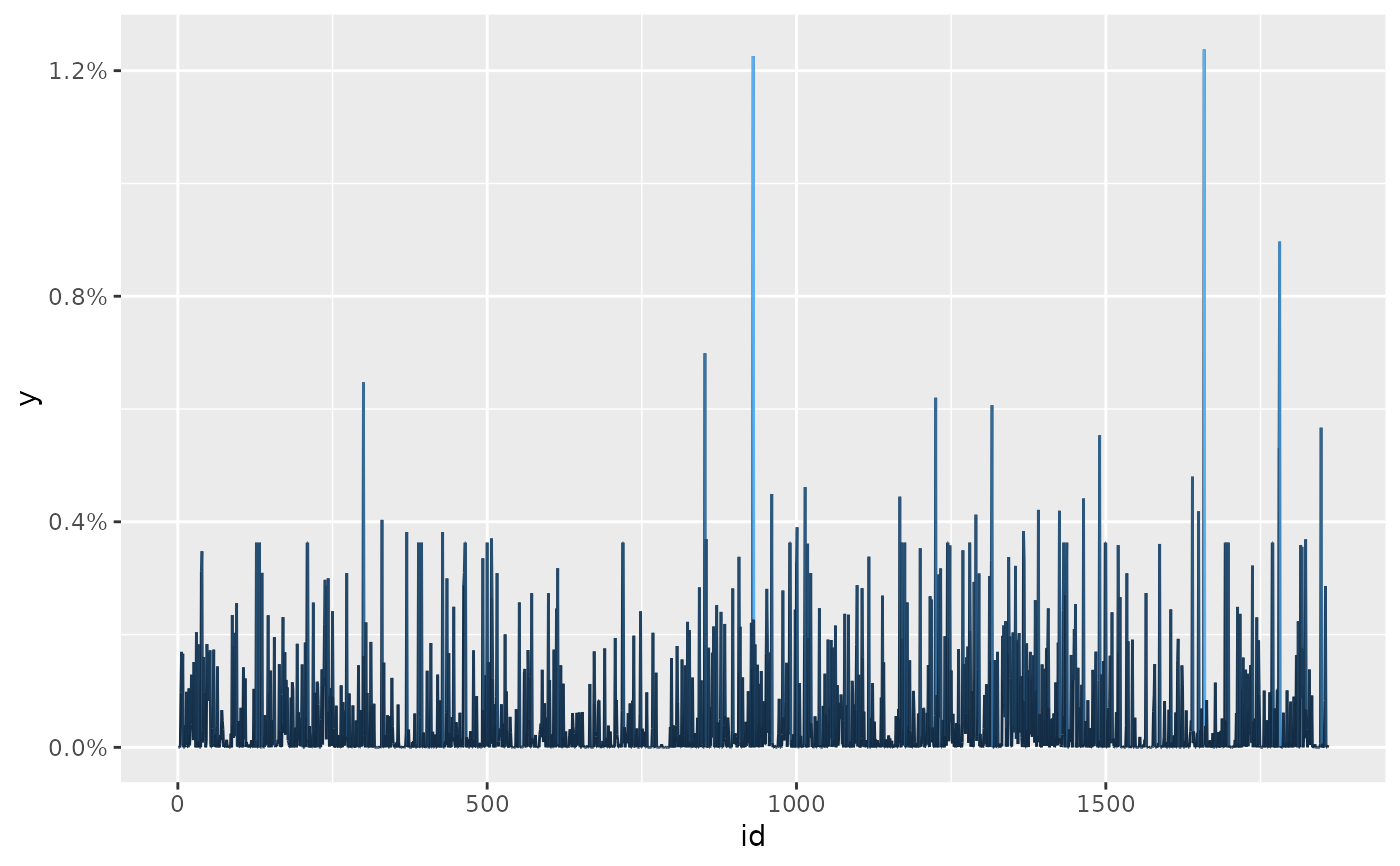# prior correlation structure
stats::cor(ret)
#>            DAX       SMI       CAC      FTSE
#> DAX  1.0000000 0.7031219 0.7344304 0.6394674
#> SMI  0.7031219 1.0000000 0.6160454 0.5847791
#> CAC  0.7344304 0.6160454 1.0000000 0.6485679
#> FTSE 0.6394674 0.5847791 0.6485679 1.0000000

# posterior correlation structure matches the initial view very closely
stats::cov2cor(ffp_moments(x = ret, p = ep)$sigma)
#>            DAX       SMI       CAC      FTSE
#> DAX  1.0000000 0.9509531 0.9538418 0.9494368
#> SMI  0.9509531 1.0000000 0.9518980 0.9426105
#> CAC  0.9538418 0.9518980 1.0000000 0.9447604
#> FTSE 0.9494368 0.9426105 0.9447604 1.0000000