Views on Covariance Matrix

Helper to construct views on variance-covariance matrix.

Usage

view_on_covariance(x, mean, sigma)

# S3 method for default
view_on_covariance(x, mean, sigma)

# S3 method for matrix
view_on_covariance(x, mean, sigma)

# S3 method for xts
view_on_covariance(x, mean, sigma)

# S3 method for tbl_df
view_on_covariance(x, mean, sigma)

Arguments

x

An univariate or a multivariate distribution.

mean

A double for the location parameter of the series in x.

sigma

A matrix for the target variance-covariance parameter of the series in x.

Value

A list of the view class.

Examples

library(ggplot2)

# Invariant (stationarity)
ret <- diff(log(EuStockMarkets))

# Expectations for location and dispersion parameters
mean <- colMeans(ret) # No active expectations for returns
cor <- matrix(0, ncol = 4, nrow = 4) # diagonal covariance matrix
diag(cor) <- 1                       # diagonal covariance matrix
sds <- apply(ret, 2, sd)             # diagonal covariance matrix
covs <- diag(sds) %*% cor %*% diag(sds) ## diagonal covariance matrix

# prior probabilities (usually equal weight scheme)
prior <- rep(1 / nrow(ret), nrow(ret))

# Views
views <- view_on_covariance(x = ret, mean = mean, sigma = covs)
views
#> # ffp view
#> Type:  View On Covariance
#> Aeq :  Dim 10 x 1859 
#> beq :  Dim 10 x 1 

# Optimization
ep <- entropy_pooling(p = prior, Aeq = views$Aeq, beq = views$beq, solver = "nlminb")
autoplot(ep)


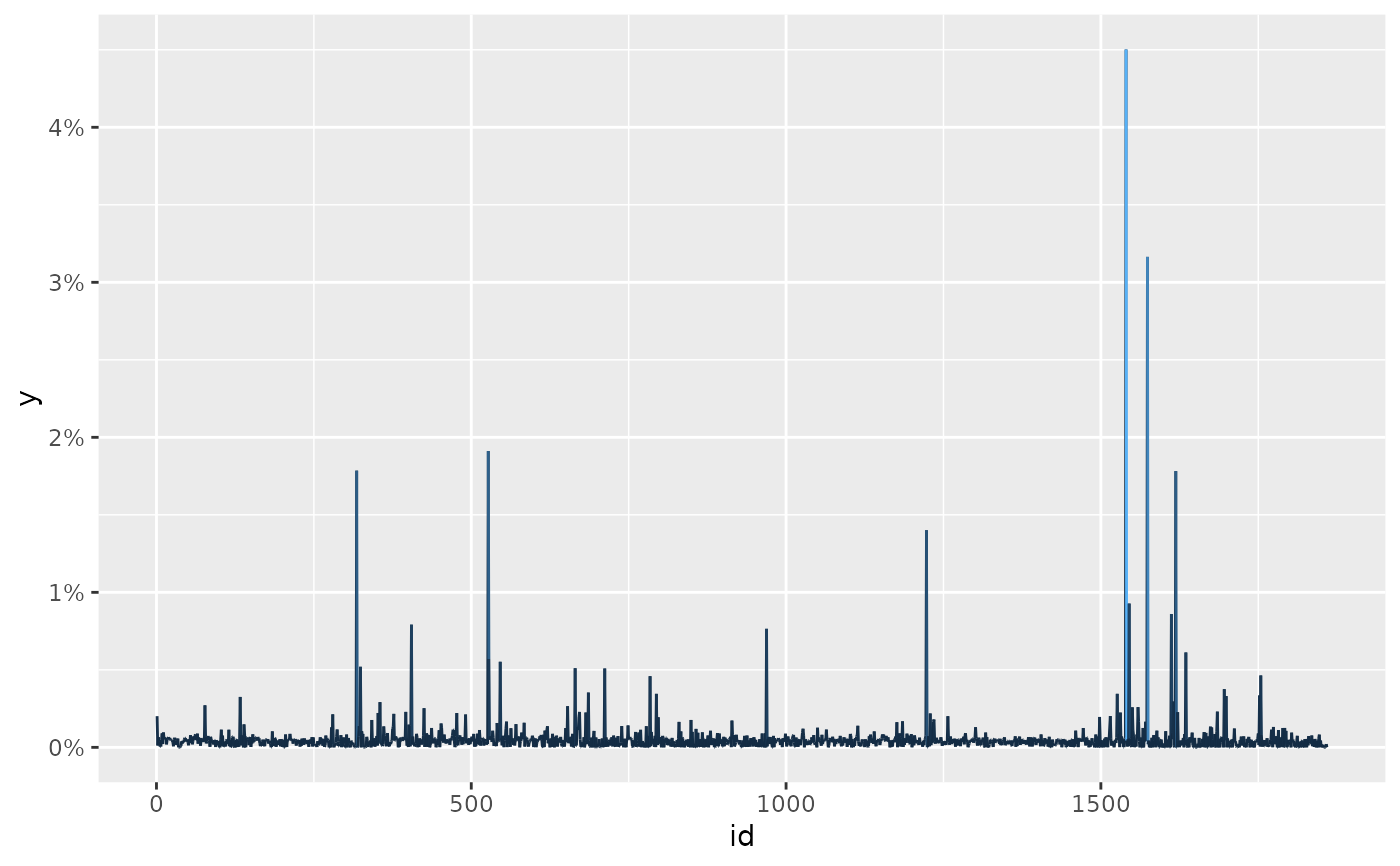# original covariance matrix
stats::cov(ret)
#>               DAX          SMI          CAC         FTSE
#> DAX  1.061072e-04 6.699564e-05 8.345130e-05 5.241794e-05
#> SMI  6.699564e-05 8.556317e-05 6.285881e-05 4.304517e-05
#> CAC  8.345130e-05 6.285881e-05 1.216802e-04 5.693174e-05
#> FTSE 5.241794e-05 4.304517e-05 5.693174e-05 6.332543e-05

# Posterior covariance matrix
ffp_moments(x = ret, p = ep)$sigma
#>                DAX           SMI          CAC          FTSE
#> DAX   1.034982e-04 -9.807377e-07 5.084087e-06 -3.943374e-06
#> SMI  -9.807377e-07  8.375999e-05 1.339814e-06 -1.440063e-06
#> CAC   5.084087e-06  1.339814e-06 1.204302e-04  9.662796e-07
#> FTSE -3.943374e-06 -1.440063e-06 9.662796e-07  6.224202e-05