Exponential smoothing twists probabilities by giving relatively more weight to recent observations at an exponential rate.
Usage
exp_decay(x, lambda)
# S3 method for default
exp_decay(x, lambda)
# S3 method for numeric
exp_decay(x, lambda)
# S3 method for matrix
exp_decay(x, lambda)
# S3 method for ts
exp_decay(x, lambda)
# S3 method for xts
exp_decay(x, lambda)
# S3 method for data.frame
exp_decay(x, lambda)
# S3 method for tbl
exp_decay(x, lambda)Details
The half-life is linked with the lambda parameter as follows:
HL = log(2) / lambda.
For example: log(2) / 0.0166 is approximately 42. So, a parameter lambda of 0.0166
can be associated with a half-life of two-months (21 * 2).
Examples
library(ggplot2)
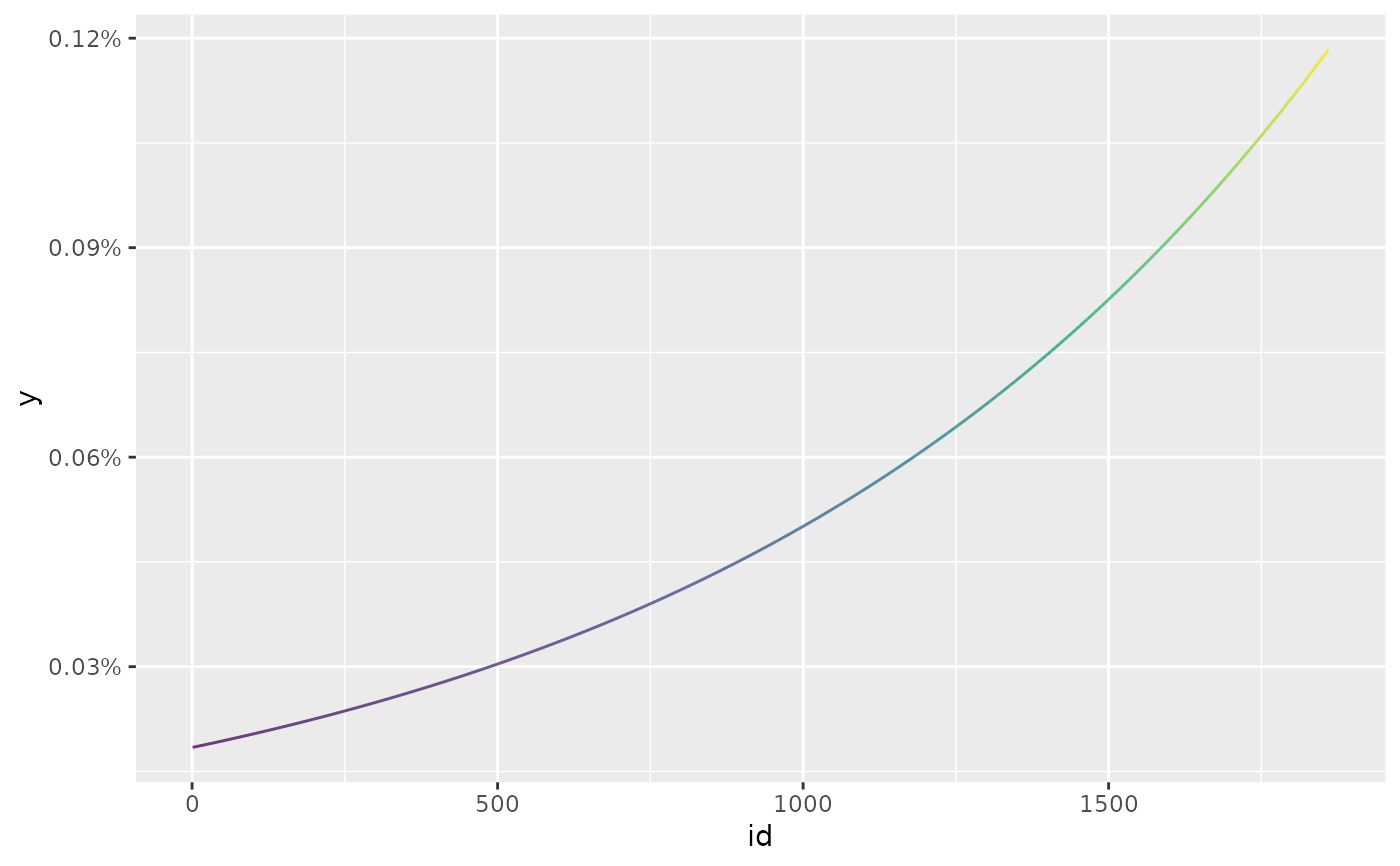
# long half_life
long_hl <- exp_decay(EuStockMarkets, 0.001)
long_hl
#> <ffp[1860]>
#> 0.0001844669 0.0001846515 0.0001848363 0.0001850212 0.0001852063 ... 0.001183783
autoplot(long_hl) +
scale_color_viridis_c()
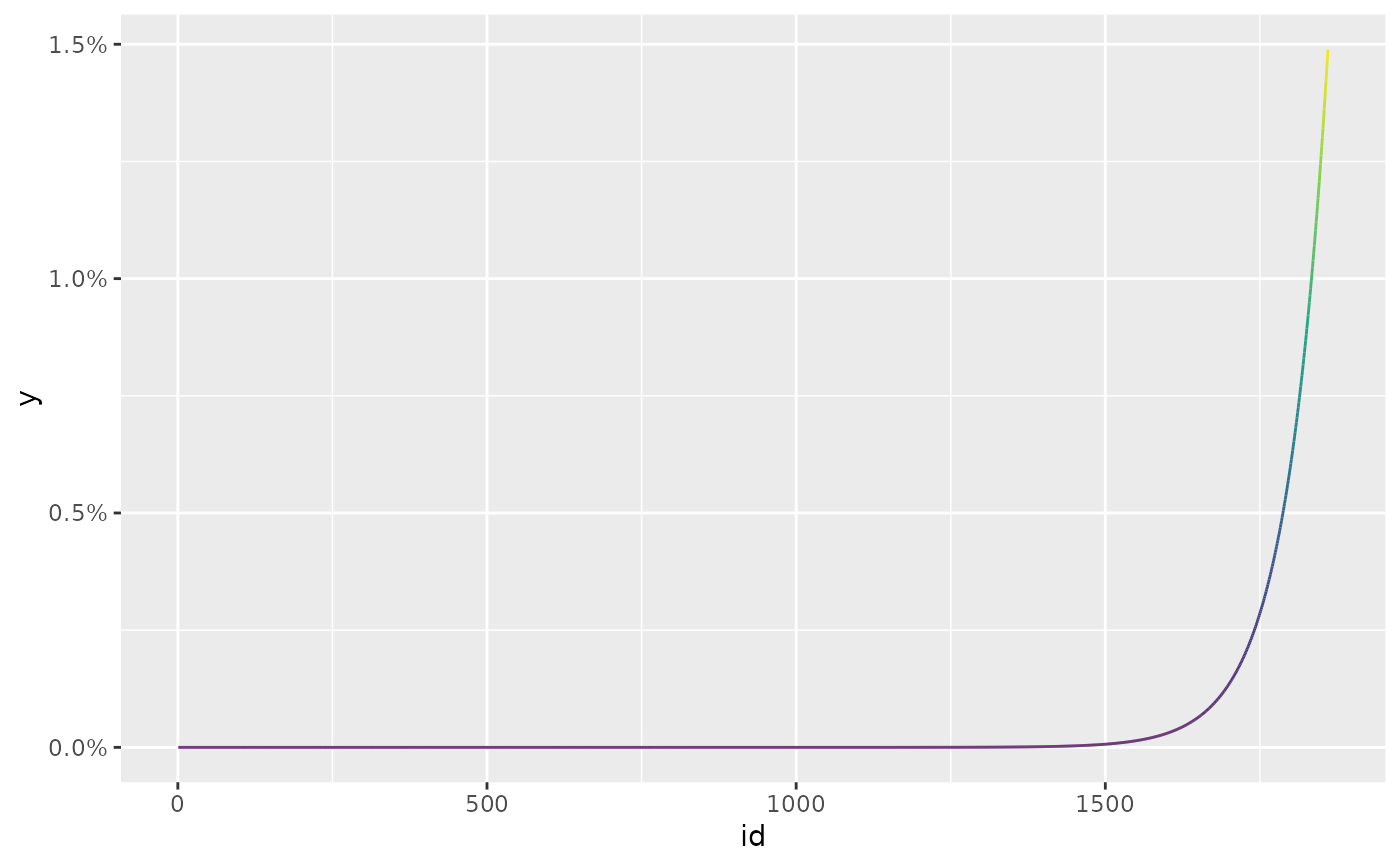
 # short half_life
short_hl <- exp_decay(EuStockMarkets, 0.015)
short_hl
#> <ffp[1860]>
#> 1.154879e-14 1.172333e-14 1.19005e-14 1.208036e-14 1.226293e-14 ... 0.01488806
autoplot(short_hl) +
scale_color_viridis_c()
# short half_life
short_hl <- exp_decay(EuStockMarkets, 0.015)
short_hl
#> <ffp[1860]>
#> 1.154879e-14 1.172333e-14 1.19005e-14 1.208036e-14 1.226293e-14 ... 0.01488806
autoplot(short_hl) +
scale_color_viridis_c()