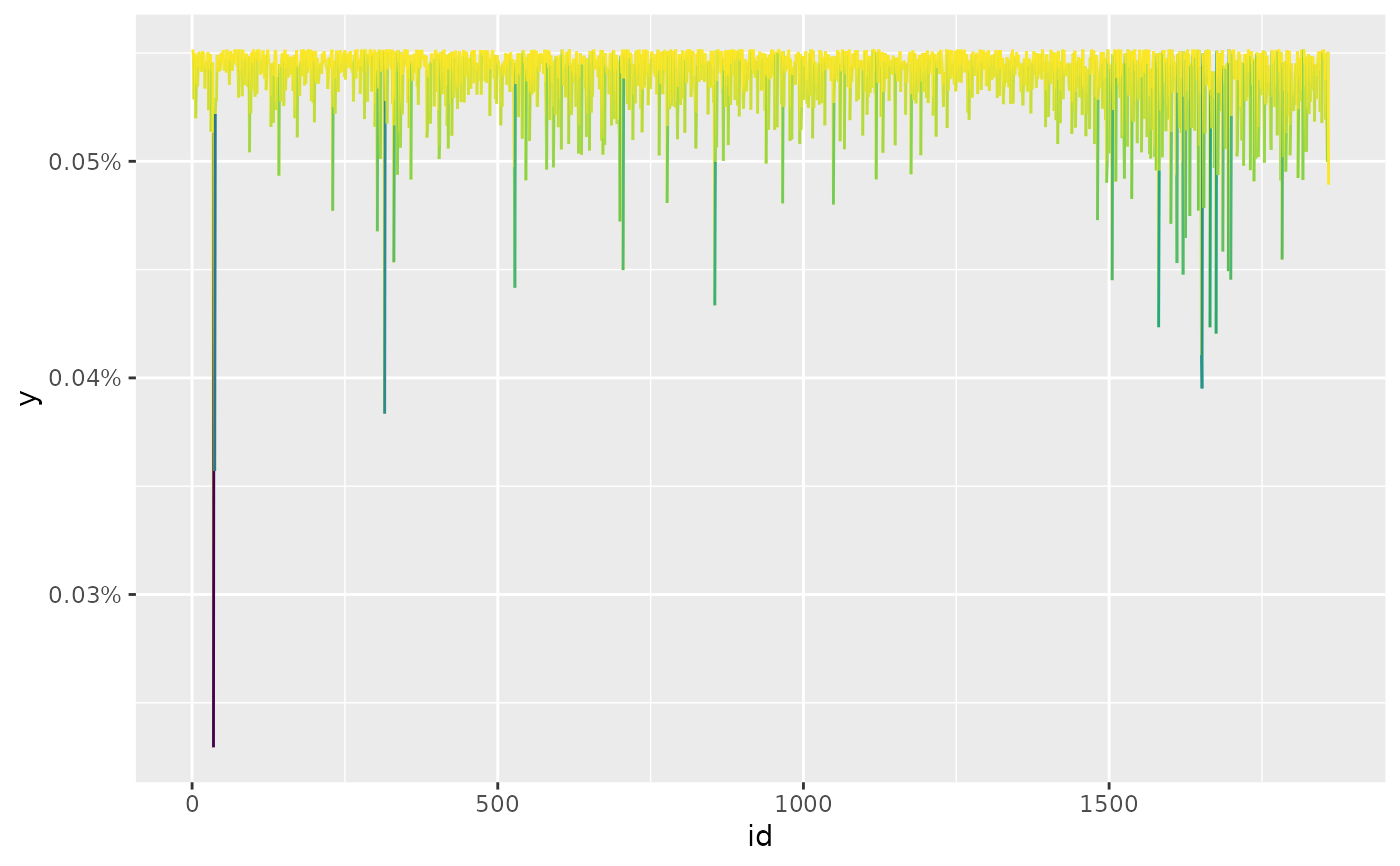
Historical realizations receive a weight proportional to their distance from a target mean.
Usage
kernel_normal(x, mean, sigma)
# S3 method for default
kernel_normal(x, mean, sigma)
# S3 method for numeric
kernel_normal(x, mean, sigma)
# S3 method for matrix
kernel_normal(x, mean, sigma)
# S3 method for ts
kernel_normal(x, mean, sigma)
# S3 method for xts
kernel_normal(x, mean, sigma)
# S3 method for tbl_df
kernel_normal(x, mean, sigma)
# S3 method for data.frame
kernel_normal(x, mean, sigma)Arguments
- x
An univariate or a multivariate distribution.
- mean
A numeric vector in which the kernel should be centered.
- sigma
The uncertainty (volatility) around the mean.
Examples
library(ggplot2)
ret <- diff(log(EuStockMarkets[ , 1]))
mean <- -0.01 # scenarios around -1%
sigma <- var(diff(ret))
kn <- kernel_normal(ret, mean, sigma)
kn
#> <ffp[1859]>
#> 0.0007806016 0.0007261808 0.0003335773 0.0006663388 0.0007309458 ... 7.07516e-05
autoplot(kn) +
scale_color_viridis_c()
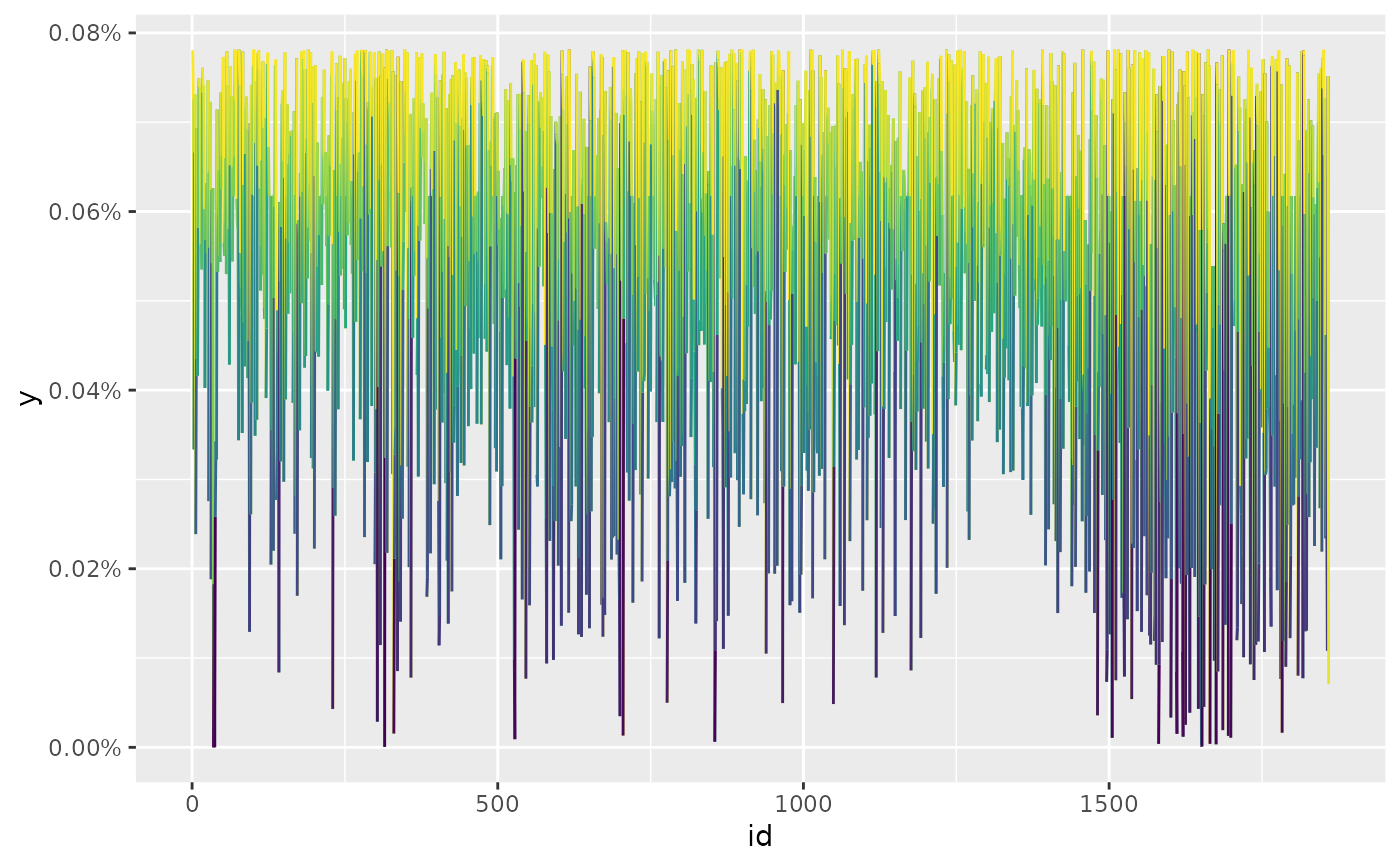 # A larger sigma spreads out the distribution
sigma <- var(diff(ret)) / 0.05
kn <- kernel_normal(ret, mean, sigma)
autoplot(kn) +
scale_color_viridis_c()
# A larger sigma spreads out the distribution
sigma <- var(diff(ret)) / 0.05
kn <- kernel_normal(ret, mean, sigma)
autoplot(kn) +
scale_color_viridis_c()